Занимательная логика: развивающие игры и упражнения для детей

Понятие мышления и его виды

Ощущение и восприятие отражают отдельные стороны явлений, моментов действительности в более или менее случайных сочетаниях.

Мышление соотносит данные ощущений и восприятий, сопоставляет, сравнивает, различает, раскрывает отношения.  Через отношения между непосредственно чувственно данными свойствами вещей и явлений мышление раскрывает новые, непосредственно чувственно не данные абстрактные их свойства: выявляя взаимосвязи и постигая действительность в этих ее взаимосвязях, оно глубже познает ее сущность.

Мышление отражает бытие в его связях и отношениях, в его многообразных опосредованиях.

Раскрытие отношений, связей между предметами составляет существенную задачу мышления: этим определяется специфический путь, которым мышление идет по все более глубокому познанию бытия. Мышление отражает не только отношения и связи, но также свойства и сущность, отношения отражаются не только в мышлении.

Мышление является высшим познавательным процессом. Оно представляет собой активную форму творческого отражения и преобразования человеком действительности. Мышление порождает такой результат, какого ни в самой действительности, ни у субъекта на данный момент времени не существует. Мышление также можно понимать как получение новых знаний, творческое преобразование имеющихся представлений.

Мышление человека осуществляется тремя способами:

1. Наглядно-действенное
2. Наглядно-образное
3. Словесно-логическое.

Наглядно-действенное мышление

Наглядно-действенное мышление характеризуется тем, что сам процесс мышления представляет собой практическую деятельность, осуществленную человеком с реальными предметами. Основным условием решения задачи в данном случае являются правильные действия с соответствующими предметами, изменяя их состояния и свойства.

Данный вид мышления является исторически наиболее ранним видом мышления человека. Именно с этого вида мышления начиналось развитие мышления у человека в процессе зарождения его трудовой деятельности. Первоначально ребенок решает задачи, непосредственно действуя с предметами. Решает с помощью реального физического преобразования ситуации, апробирования свойств объектов.

Эта форма мышления наиболее характерна для детей до 3 лет. Ребенок этого возраста сравнивает предметы, накладывает один на другой; анализирует, разламывая на части свою игрушку; синтезирует и обобщает, раскладывая кубики по цвету.

Ребенок не ставит еще перед собой цели и не планирует своих действий. Ребенок мыслит, действуя.

Однако было бы ошибочно думать, что наглядно-действенное мышление является какой-то примитивной формой мышления. Возникнув на заре человечества и появляясь у каждого человека в первые годы его жизни, оно сохраняется и развивается на протяжении всей истории человечества, на всех возрастных ступенях каждого человека.

Этот вид мышления оказывается необходимым и незаменимым во всех тех случаях, когда наиболее целесообразным оказывается решение мыслительной задачи непосредственно в процессе практической деятельности.

Наглядно-образное мышление

Отличительная особенность следующего вида мышления – наглядно-образного состоит в том, что мыслительный процесс в нем непосредственно связан с восприятием мыслящим человеком окружающей действительности, а сами необходимые для мышления образы представлены в его кратковременной и оперативной памяти.

Это мышление характеризуется тем, что здесь содержание мыслительной задачи основано на образном материале, связано с оперированием образами. Оно наиболее полно воссоздает все многообразие различных фактических характеристик предмета.

В образе может быть одновременно зафиксировано видение предмета с нескольких точек зрения. В простейшей форме наглядно-образное мышление проявляется у детей в возрасте 4-7 лет. Ребенку необходимо отчетливо воспринимать и наглядно представлять данный объект. Все их доказательства носят наглядный конкретный характер.

Наглядно-образное мышление – вид мышления, который осуществляется на основе преобразований образов восприятия в образы-представления, дальнейшего изменения преобразования и обобщения предметного содержания реальности в образно-концептуальной форме.

A.З. Зак отмечает, что наглядно-образное мышление используется человеком для выяснения отношений, он оперирует лишь в мысленном плане, с образами предметов, если предметы имеются в данный момент или с их представлениями, если предмет отсутствует.

Словесно-логическое мышление

Словесно-логическое мышление осуществляется при помощи логических операций. Используя словесную форму, человек оперирует наиболее отвлеченными понятиями, подчас такими, которые вообще не имеют прямого образного выражения (понятия, термины).

Именно этот вид мышления позволяет установить наиболее общие закономерности, определяющие развитие природы и общества самого человека. Благодаря этому виду мышления человеку удается наиболее обобщенно решать мыслительные задачи.

Используя словесную форму, человек оперирует наиболее отвлеченными понятиями, подчас такими, которые вообще не имеют прямого образного выражения.

Словесно-логическое мышление – один из видов мышления, характеризующийся использованием понятия логических конструкций. Словесно-логическое мышление функционирует на базе языковых средств.

В структуре словесно-логического мышления формируются и функционируют различные виды обобщений.

При таком мышлении для выявления отношения человек использует слова, а не сами предметы или его образы, которые лишь обозначают предметы, строит из этих слов суждения, которые связывают по правилам логики, от общих суждений переходит к частным.

Большую часть знаний об окружающей нас действительности мы получаем с помощью рассуждений, поэтому умение правильно рассуждать и строить выводы является одним из важнейших логических умений, необходимых человеку в любой области деятельности.

Главная цель при развитии логического мышления заключается в том, чтобы с его помощью сформировать у детей умение рассуждать, делать выводы из тех суждений, которые предлагаются в качестве исходных, умение ограничиваться содержанием этих суждений и не привлекать других соображений, связанных с внешними особенностями тех вещей или их образов, которые отражаются и обозначаются в исходных суждениях.

Логическое мышление обнаруживается, прежде всего, в протекании самого мыслительного процесса. В отличие от наглядно-образного и наглядно-действенного мышления логическое мышление осуществляется только словесным путем.

Логическое мышление характеризуется обычным умением вычленять частные случаи из некоторого общего положения, умением теоретически предсказывать конкретные результаты, обобщать полученные выводы и т.д.

Развитие логического мышления является, прежде всего, развитием теоретического мышления.

Все перечисленные виды мышления у человека сосуществуют и могут быть представлены в одной и той же деятельности.

Формы мышления

Многие виды мышления оперируют такими логическими формами как:

• понятие
• суждение
• умозаключение

Понятие

Понятие – это форма мышления, отражающая существенные свойства, связи, отношения предметов и явлений.  Основная логическая функция понятия – выделение общего, которое достигается посредством отвлечения от всех особенностей отдельного предмета данного класса. В логике – мысль, в которой обобщаются и выделяются предметы некоторого класса по определённым общим и в совокупности специфическим для них признакам.

Понятия – это высший уровень обобщения, они отражают большинство наших представлений о мире. Например, мебель, дикие и домашние животные, средневековый период – это все понятия, относящиеся к разным аспектам нашего знания.

Понятие – форма мышления, в которой отражаются существенные признаки отдельного предмета или класса однородных предметов. Понятия в языке выражаются словами, например: портфель, ботинки и др.

Признаки предмета могут быть существенными и несущественными.
В понятиях отражается совокупность существенных признаков, т.е. таких, каждый из которых, взятый отдельно, необходим, а все вместе  достаточны, чтобы с их помощью можно было отличить данный предмет от всех остальных.

Признаки бывают отличительные и неотличительные.
Есть признаки, присущие только одному предмету, они позволяют отличить его от других сходных с ним предметов. Например, отличительным единичным признаком планеты Меркурий является то, что её орбита наименее удалена от Солнца по сравнению с другими планетами Солнечной системы.

Суждение

Суждение отражает связь между двумя понятиями. Суждения, исследуемые психологией, связаны с утверждением или отрицанием чего-либо и выражаются в форме предложений. Фраза «Вода замерзает при нулевой температуре» отражает суждение о свойствах воды. При этом суждение понятно только в том случае, когда человек имеет представление о тех понятиях, о которых он судит, т.е. понимает, чем различаются вода и лёд.

Таким образом, знание о предмете связано с возможностью высказать о нём правильное (с точки зрения общечеловеческого опыта) суждение.

Суждение – форма мышления, в которой что-либо утверждается или отрицается о предметах, признаках или их отношениях.

Например, «ученик Иванов – отличник»; «все металлы – проводники электричества».

Умозаключение

Под рассуждением или умозаключением понимают логическую операцию, посредством которой из одного или нескольких утверждений, получается новое по отношению к исходным утверждениям. Оно называется заключением / следствием / выводом.

В словесных формулировках заключение отделяется от утверждений с помощью слов «следовательно», «значит» и др.

Например, 1-е суждение: «Если число оканчивается 0 или цифрой 5, то оно делится на 5». 2-е суждение: «Число 25 заканчивается цифрой 5». Заключение: «Число 25 делится на 5».

Умозаключения бывают разные.
В одних идут от частного к общему, в других – наоборот. В одних умозаключениях, вывод с необходимостью следует из утверждений, в других – имеет лишь некоторую степень достоверности.

В логике существуют различные классификации умозаключений

В основе классификации умозаключений лежит отношение логического следования.

В этом случае все умозаключения делятся на:

• дедуктивные
• недедуктивные

Дедуктивными при такой классификации называются умозаключения, между утверждением и заключением которых имеет место отношение логического следования.

Недедуктивными в этом случае называют все умозаключения, в которых нет логического следования между утверждением и заключением.

Например, математика – наука дедуктивная. Это означает, что предложения, формируемые в рамках какой-либо ее теории, доказываются в ней строго логическим путем на основе некоторых исходных данных.

Умозаключение будем называть индуктивным, если на основании того, что некоторые объекты какой-либо группы обладают определенным свойством, делается вывод, что этим свойством обладают все объекты данной группы.

Овладение формами мышления является важным показателем развития мышления ребенка.

Логические приемы мышления

В структуре мышления выделяют следующие логические приемы мышления – логические операции:

• анализ
• синтез
• абстракция
• обобщение
• сравнение
• конкретизация
• классификация

Сравнение

Сравнение – наиболее элементарная и в то же время чрезвычайно существенная мыслительная операция. Она строится на составлении двух или нескольких однородных, но разных предметов.

Для того, чтобы установить сходство и различие двух (или нескольких) предметов, человек мысленно дробит каждый из них на части, выделяет их признаки (анализ) и, сопоставляя, устанавливает их совпадение или различие (синтез).

Путем сравнения дети легче устанавливают общее в разном и различное в сходном.

Сравнение у детей, как синтез и анализ, имеет ряд особенностей.

Особенностью является то, что часто подменяют сравнение простым рядоположением предметов: сначала ребенок рассказывает, что знает об одном предмете, явлении, а потом – о другом.

Нередко дети затрудняются сравнивать предметы и явления потому, что они не могут самостоятельно составить план сравнения, поэтому необходимо вести целенаправленную работу по формированию у них приема сравнения.

Сравнение есть основа всякой мыслительной группировки предметов, явлений, событий.

Классификация

Классификация производная от сравнения и более сложная операция. На основе сходства основных признаков или более частных сторон, предметы объединяются в группы: классы, рода, виды.

При проведении классификации надо помнить о следующих правилах:

1. В одной и той же классификации необходимо применять только одно основание.
   Основание – признак, по которому данные предметы делятся на группы или классы. Например, множество натуральных чисел можно разбить на четные и на нечетные числа, а по другому основанию – на простые и составные числа.
   
2. Члены классификации должны взаимно исключать друг друга. Например, все члены являются либо четными числами, либо нечетными.
3. Объем членов классификации должен равняться объему классифицируемых объектов. То есть, все предметы, которые даны, после проведенной классификации должны быть отнесены к какому-либо классу. Например, объединение множества четных чисел и множества нечетных чисел должно совпадать со всем множеством натуральных чисел.
4. Подразделение на классы в проводимой классификации должно быть непрерывным, то есть необходимо брать ближайший подкласс и не перескакивать в более отдаленный подкласс, иначе не все классифицируемые объекты станут членами такой классификации. Следовательно, она будет проведена неверно.

Логическое действие – классификация по своей структуре является сложным действием и включает ряд отдельных операций:

• выделение основания классификации;
• разделение объектов на классы по заданному основанию;
• отнесение объекта к классу;
• словесная характеристика каждого класса;
• контроль результатов проведенной классификации.

Анализ

Анализ – дробление, членение какого-то целого на части, дифференцировка, выделение какой-либо стороны, отдельных частей, признаков.

Развитие анализа идет от практически действенного к чувственному и в дальнейшем к умственному.

У детей преобладающим является практически-действенный и практический анализ.

Развитие анализа проходит ряд этапов: от частного к комплексному и системному.

Преобладающим видом анализа у дошкольников является частичный, у младших школьников – частичный и комплексный. Очень часто дети анализируют отдельные части или свойства предмета.

При комплексном анализе, например, усвоение учебного материала более полное, так как дети рассматривают более или менее все части или свойства изучаемого предмета, но взаимосвязи между ними еще не устанавливают, т.е. они просто перечисляют в определенной последовательности выделяемые части или свойства предмета.

На следующем этапе развития анализа младшие школьники производят уже системный анализ изучаемых предметов и явлений. Они располагают части и свойства предметов в определенной системе.

Синтез

Синтез – соединение частей, сторон признаков, группировка какого-то целого.

Несмотря на то, что анализ как будто противоположен синтезу, они никогда не существуют обособленно друг от друга, но составляют две стороны единого процесса или способа мышления. Именно взаимосвязь и взаимозависимость анализа и синтеза и составляют суть, ядро мыслительного.

Взаимоотношения анализа и синтеза выражены в следующих зависимостях:

1. Анализ целого есть в то же время и его синтез, поскольку изучение, размышление над каким-то целым (событием, явлением, предметом) есть анализ, который направляется, не только на выделение частей сторон, признаков целого, но одновременно и на выделение связей, зависимостей, отношений, существующих между этими частями единого целого.
2. Процесс мышления может проходить на различном уровне: он осуществляется либо непосредственным действием с предметами, их практическим расчленением и соединением, либо задача может быть дана в наглядной форме.

Систематизация – группировка предметов или явлений, но уже не столь по сходству их основных признаков, с такими же предметами целого класса, но и выделение в этой группе более мелких подгрупп, видов, разрядов.

Обобщение

Обобщение – мысленное объединение предметов и явлений на основе сходства их существенных признаков и отвлечениях от признаков второстепенных, несущественных.

Как показывают исследования, учащиеся 1 и 2 классов выделяют существенные, наиболее заметные внешние признаки предметов. Характеризуя предметы, дети этого возраста говорят, прежде всего, о разнообразных действиях самих предметов и о своих действиях с ними. То есть объединяют предметы не по их общим признакам, а по некоторым причинно-следственным связям и по взаимодействию предметов.

Установлено три уровня обобщения у детей:

1. Чувственное
2. Практически-действенное
3.  Образно-понятийное и понятийно-образное

Развитие обобщения у детей идет от широкого, но все более к дифференцированному.

Обобщением является любое правило, любой закон, выведение на основе наблюдений одних и тех же фактов, явлений или закономерностей в разных условиях, на разном содержании любое понятие, которым пользуются взрослые люди, понятие числа, морали, этики также есть обобщения. Это всегда какой-то итог, общий, совершаемый человеком, на основе ряда, в чем-то однородных фактов, явлений, поступков людей.

Абстракция

Абстрагирование – как известно, заключается в мысленном отвлечении от ряда сторон и признаков объекта и выделение тех признаков, которые нужны в зависимости от ситуации.

Абстрагирование является такой мыслительной операцией, без которой невозможно овладение представлениями и понятиями.

Развитие логического мышления предполагает использование операции абстрагирования.

Научить детей абстрагированию, значит выработать у них умение видеть общее, неизменно повторяющиеся, притом действительно существенные признаки большого круга. Для этого важно отбирать для наблюдения относительно большое число объектов, что дает возможность судить о подлинной общности выделяемых признаков.

Одной из особенностей абстракции детей, является то, что за существенные признаки они порой принимают внешние, яркие, часто воспринимаемые признаки.

Другая особенность заключается в том, что дети абстрагируют свойства предметов и явлений, чем связи и отношения, которые существуют между ними.

Зная эти особенности, взрослый должен обращать внимание детей на скрытые, но существенные признаки, их связи и отношения.

В этой работе, как во всяком обучении, важно соблюдение принципа перехода от простого к сложному. Поэтому целесообразно при формировании нового представления или понятия первоначально давать детям такие совокупности объектов, в которых существенные признаки были очевидными.

Конкретизация

Развитию логического мышления детей способствуют переходы от абстрагирования к конкретизации.

В основе операции конкретизации лежит процесс восхождения от абстрактного к конкретному.

Например, для дошкольников и младших школьников наиболее распространенным видом конкретизации является опознание на конкретном материале, выраженное в понятиях и правилах закономерностей.
Чем чаще на занятии, на уроке переходы от конкретного к абстрактному и от абстрактного к конкретному, тем осознаннее и глубже усваивается программный материал.

Закономерности

Закономерность – это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.

В чем смысл игры?

Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.

Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.

Как научить ребенка находить закономерности?

Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.

В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.

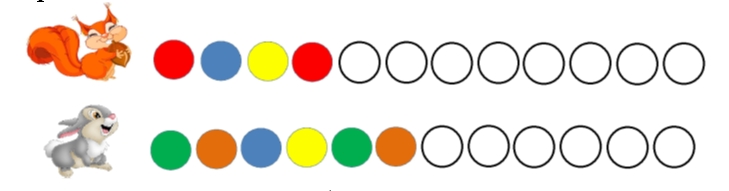
Задание 1. Раскрась дорожки для зайчика и белочки, сохраняя закономерность.

Решение:
Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.

В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.

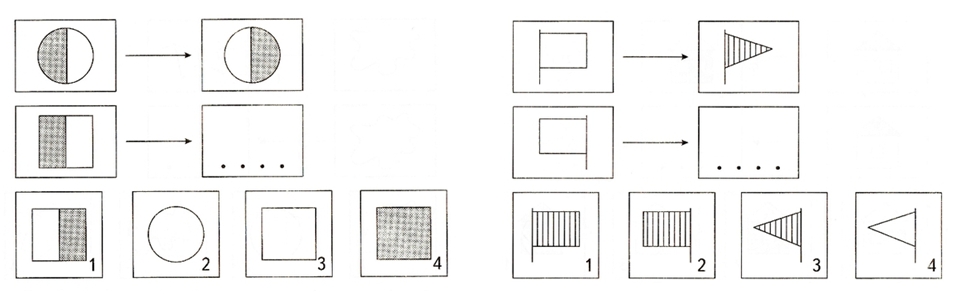
Задание 2. Найди закономерность в ряду геометрических фигур.

Решение:
В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.

Задание 3. Нарисуйте в четвертом квадрате правильный ответ.

Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки. В этой задаче имеет значение только расположение кругов квадрате. Таким образом, в последний квадрат мы должны нарисовать один синий круг в нижнем левом углу.

 

Задание 4. Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
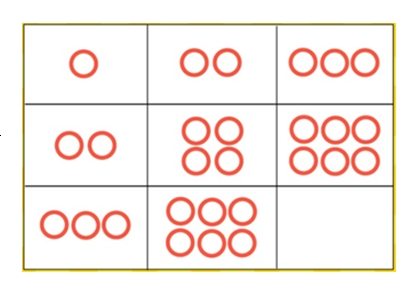Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2. Таким образом, можно предположить, что в третьем ряду количество кругов будет увеличиваться на 3 и ответ будет 9. Можно заметить, что и в вертикальных рядах эта закономерность повторяется.

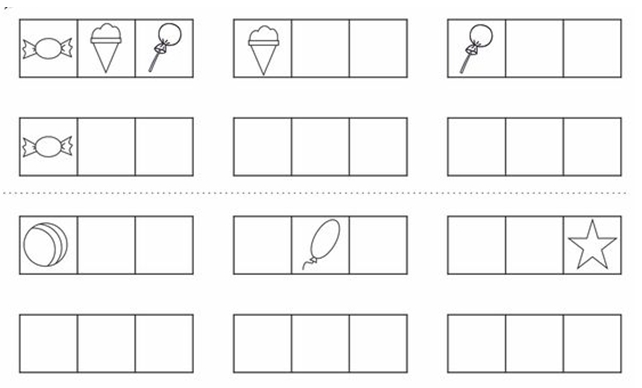
Задание 5. В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
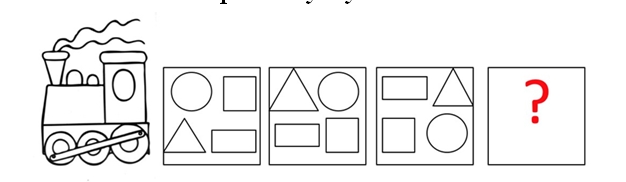Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.

Задание 6. В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.

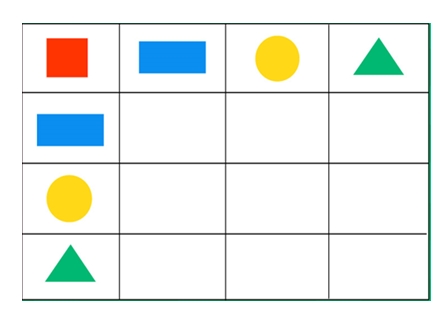
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат  и т. д.

Задание 7. Найди ошибку в бусах.

Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.

Задание 8. Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:
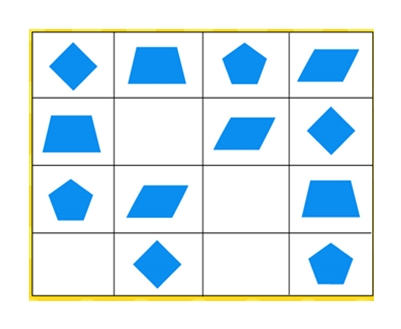Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм. Во втором ряду недостает шестиугольника, в третьем – ромба, в четвертом – параллелограмма и трапеции.

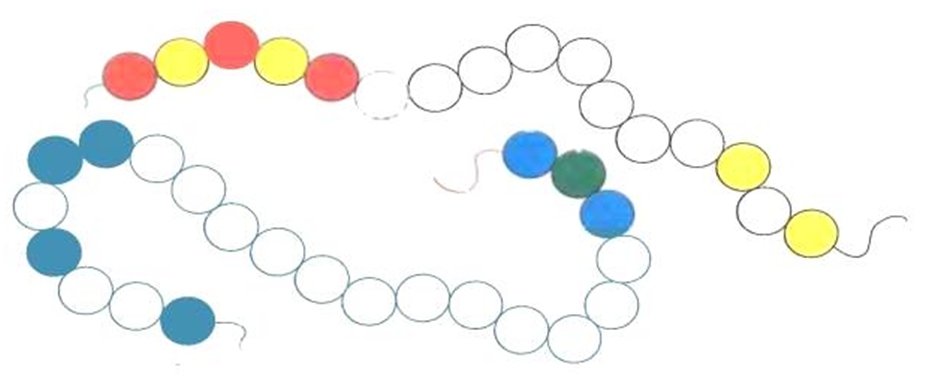
Задание 9. Какого цвета должны быть нераскрашенные бусинки? Раскрась их.

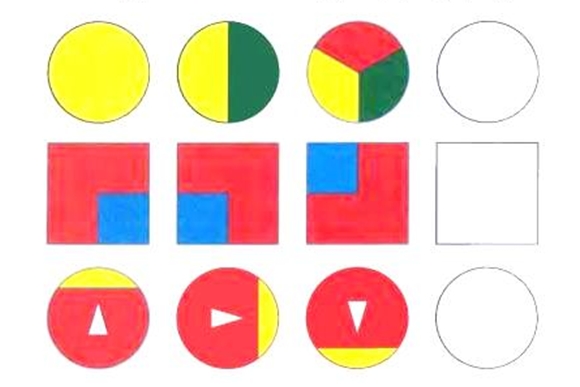
Задание 10. Дорисуй следующие фигуры, соблюдая порядок.

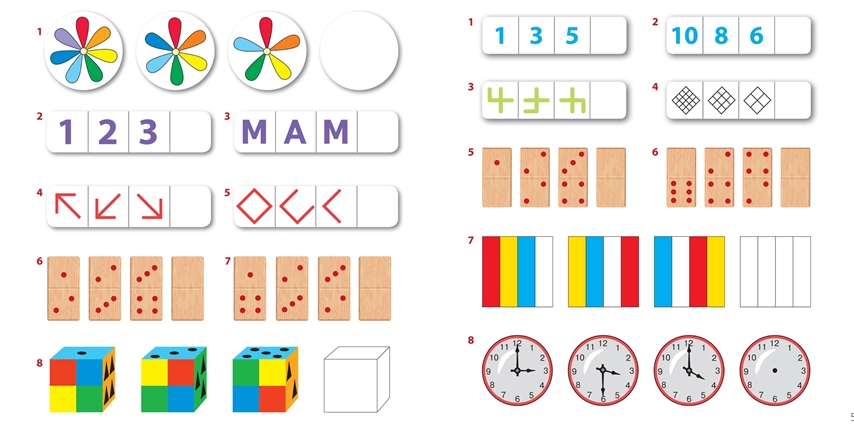
Задание 11. Дополни логические ряды.

Классификация

Дидактические игры на классификацию предметов являются очень важным инструментом для расширения и активизации словаря. По умению ребенка классифицировать предметы по группам, подбирать для группы предметов обобщающие слова можно судить об уровне его интеллектуального развития, о степени развития его речи, памяти, мышления.

На начальном этапе ребенку предлагается выбрать предметы по образцу. Задача выбрать из предложенной группы предметы, ориентируясь на их свойства: форму, цвет, размер.

В предметной классификации ребенок ориентируется уже не на внешний вид предмета, а на его назначение, например, предметы, предназначенные для приготовления и употребления пищи – посуда.

Для классификации или обобщения предметов ребенок включает мыслительные операции, благодаря которым находит основание для определения предметов или явлений в нужную группу.

Игры и упражнения на классификацию очень важны для развития ребенка. Благодаря им воспитывается речевая активность, гибкость мышления. Ребенок начинает понимать, что можно использовать различные виды классификации.

По мере того какие у предмета связи и отношения с другими предметами, он может находиться совершенно в разных группах, в соответствии с тем, какой признак будет определяющим. Задача взрослых показать малышам, что свойства предметов могут меняться, а в зависимости от этого изменится и положение предмета в группе.

Рассмотрим игры, направленные на формирование умения классификации и обобщения предметов.

Логические задачи для детей «Зачеркни лишний предмет» направлены на развитие внимания ребенка.

Ребенок должен иметь полное представление о том, что такое общий признак предмета, уметь формировать предметы в группы и давать им правильное название.

Очень важно задавать детям вопросы в процессе занятий: почему он вычеркивает тот, либо иной предмет, к какой группе он может его привязать и почему.

Внутри круга нарисуй крестики, внутри квадрата – поставь точки, внутри круга и квадрата – звездочки.

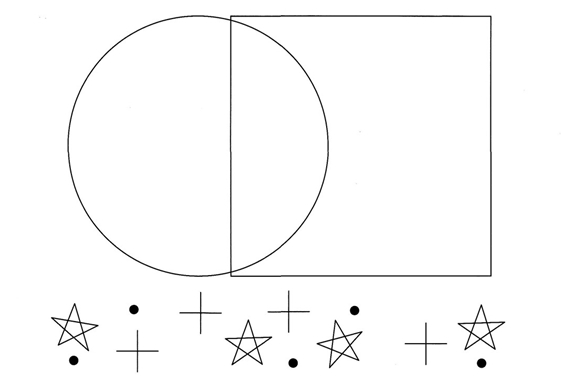
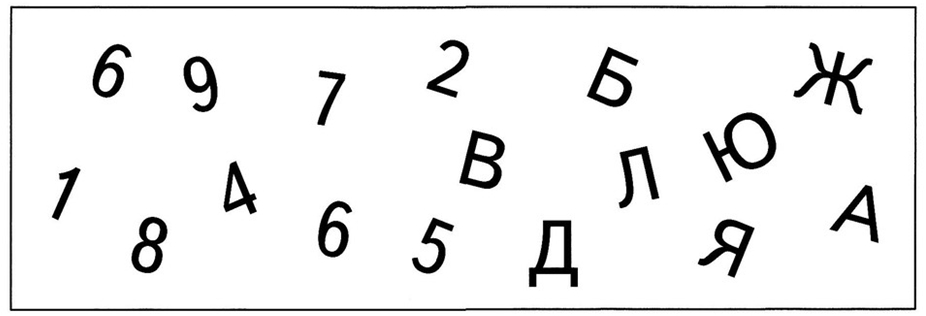
Проведи линию так, чтобы на одной части листа оказались цифры, а на другой – буквы.

Найди лишний предмет. Объясни свое решение.

Как можно назвать одним словом каждую группу предметов? Напиши.
В какой комнате живет каждая девочка?

Найди пару каждой рукавичке. Соедини их линией.

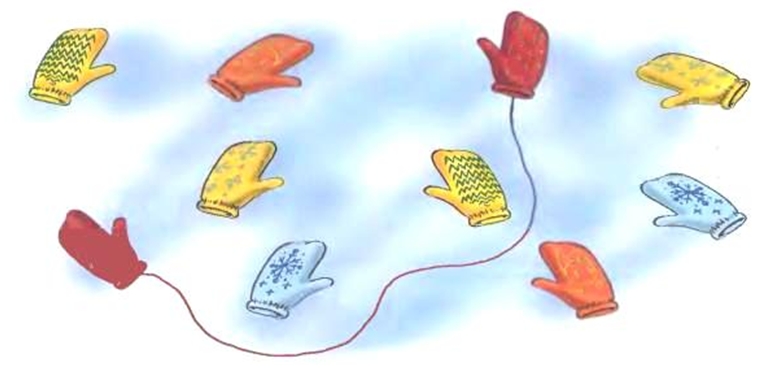
Дидактическая игра «Что я загадала?»
Цель: развивать мышление.
Игровой материал и наглядные пособия: 10 кругов разного цвета и размера.

Педагог раскладывает перед ребенком 10 кругов разного цвета и размера, предложить ребенку показать тот круг, который загадал взрослый. Объяснить правила игры: отгадывая, можно задавать вопросы, только со словами больше или меньше.

Например:

• Это круг больше красного? (Да.)
• Он больше синего? (Да.)
• Больше желтого? (Нет.)
• Это зеленый круг? (Да.)

Дидактическая игра «Посади цветы»
Цель: развивать мышление.
Игровой материал и наглядные пособия: 40 карточек с изображениями цветов с разной формой лепестков, размера, цветом сердцевины.

Педагог предлагает предложить ребенку «рассадить цветы на клумбах»: на круглую клумбу все цветы с круглыми лепестками, на квадратную – цветы с желтой сердцевиной, на прямоугольную – все большие цветы.

Вопросы: Какие цветы остались без клумбы? Какие могут расти на двух или трех клумбах?

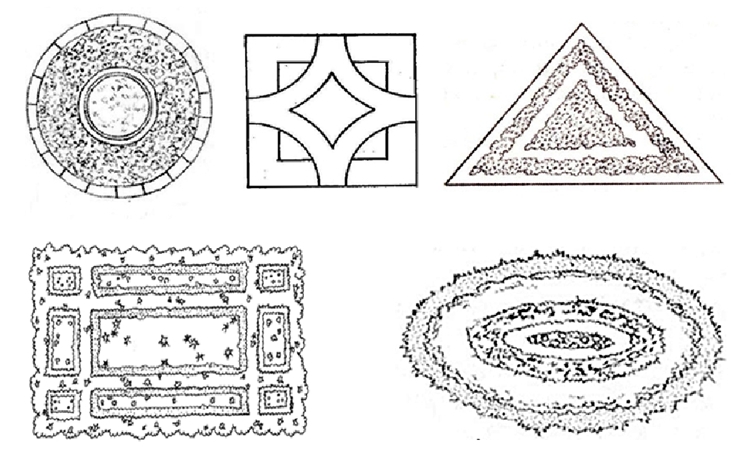
Дидактическая игра «Группируем по признакам»
Цель: закреплять умение употреблять обобщающие понятия, выражая их словами.
Игровой материал и наглядные пособия: карточки с изображением предметов (апельсин, морковь, помидор, яблоко, цыпленок, солнце).

Педагог раскладывает перед ребенком карточки с изображением разных предметов, которые можно объединить в несколько групп по какому-либо признаку. Например, апельсин, морковь, помидор, яблоко – продукты питания; апельсин, яблоко – фрукты; морковь, помидор – овощи; апельсин, помидор, яблоко, мяч, солнце – круглые; апельсин, морковь – оранжевые; солнце, цыпленок – желтые.

Шифровки

Дидактическая игра «Раскрась флаги»
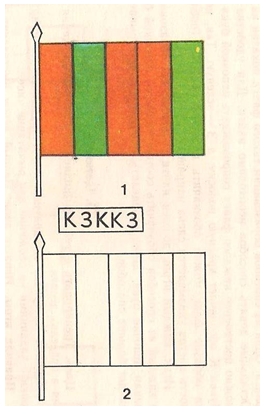Цель: упражнять детей в образовании и подсчете тех или иных комбинаций предметов.
Игровой материал: цветные карандаши, вырезанные зеленые и красные полоски, цепочки из букв К и 3.

Играют двое. Каждый играющий должен с помощью пяти  полосок – трех  красного  цвета  и  двух  зеленого  цвета – выложить флаги. Один из способов образования такого флага показан на рисунке.

Остальные девять способов необходимо найти. Для удобства сравнения можно построение каждого флага сопровождать цепочкой букв К и 3, где буква К обозначает красную полоску, а 3 – зеленую. Так, построенный на образце флаг можно обозначить цепочкой КЗК.КЗ (последовательность цветов указывается слева направо).

Каждый игрок должен найти свои способы образования флага и каждый из способов обозначить соответствующей цепочкой букв. Сравнивая цепочки букв, легко определить победителя. Выигрывает тот, кто найдет больше способов.

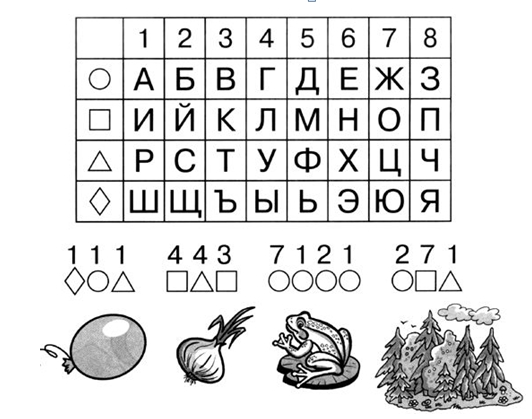
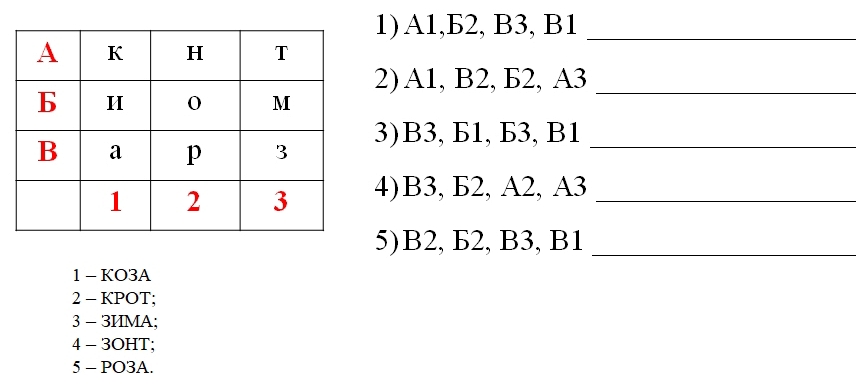
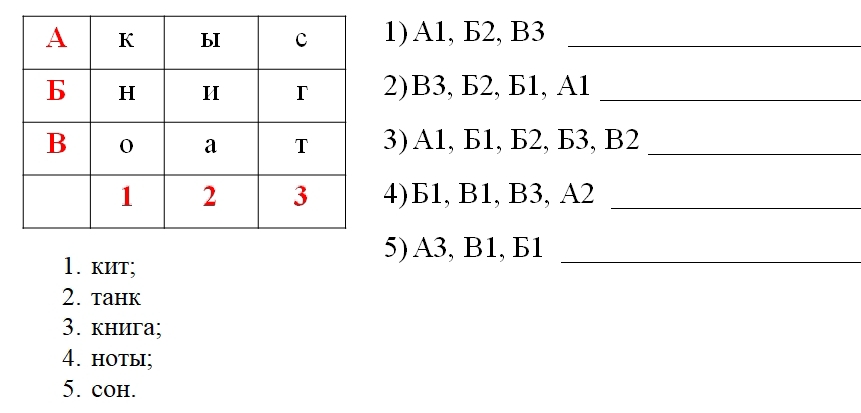
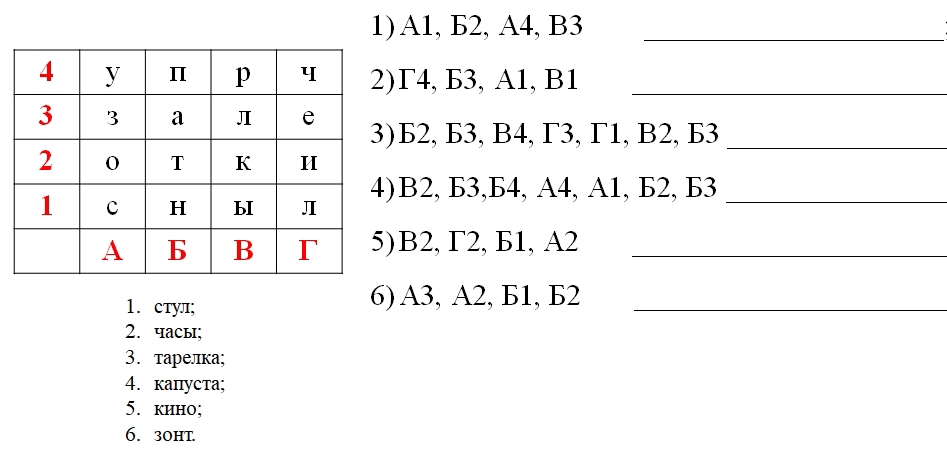
Дидактическая игра «Расшифруй слова»

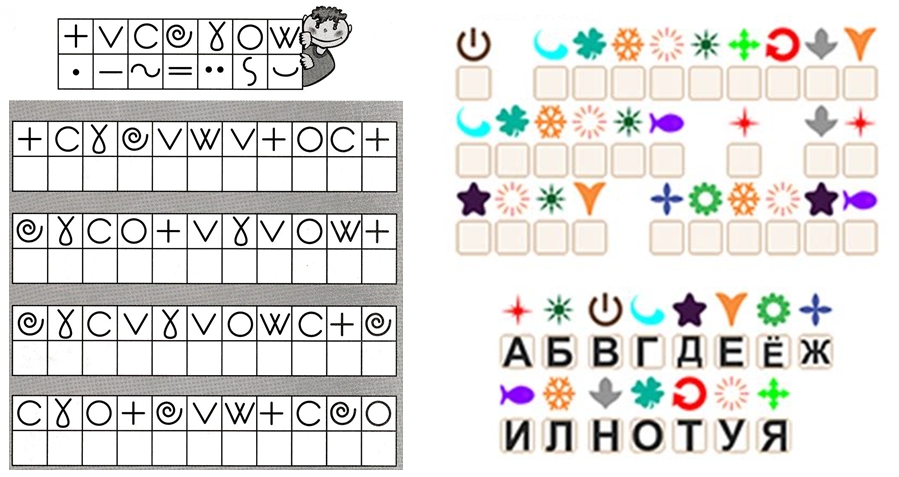
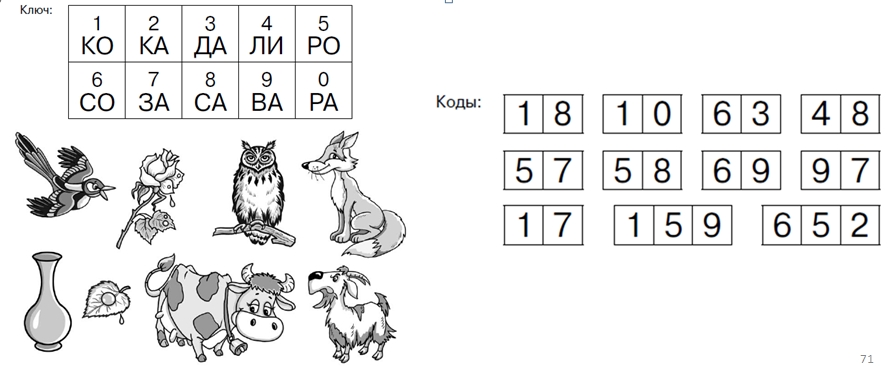
Дидактическая игра «Кодовый замок»
В каждой цифре замка закодирован слог. Какие слова получатся, если выбрать разные коды?

Дидактическая игра «Шифровальщик»
Рассмотри кодовую таблицу. Закодируй слова «дискета». Закодируй слово «монитор» и др.

Дидактическая игра «Шифровка с помощью ключа»
Возраст: игра для детей старшего дошкольного возраста (6-7 лет).
Цель: развитие концентрации и переключения внимания.
Задачи: 
— закреплять умение переключаться с одного объекта на другой;
— закреплять знание букв русского языка;
— закреплять навык чтения;
— развивать память, внимание, логическое мышление.
Ожидаемые результаты: ребенок может соотнести цифры и назначенные им буквы и прочитать зашифрованные слова.

Умозаключения и логические цепочки

Дидактическая игра «Логические концовки»
Цель: развивать логическое мышление, воображение, способность к анализу.

Детям предлагается закончить предложения:
Если стол выше стула, то стул … (ниже стола).
Если 2 больше одного, то один … (меньше двух).
Если Саша вышел из дома раньше Сережи, то Сережа … (вышел позже Саши).
Если река глубже ручейка, то ручеек … (мельче реки).
Если сестра старше брата, то брат … (младше сестры).
Если правая рука справа, то левая … (слева).

Дидактическая игра «Найди варианты»
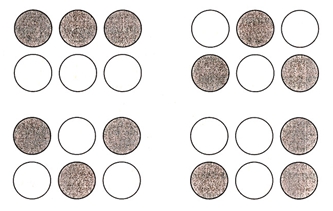Цель: развивать логическое мышление, сообразительность.
Игровой материал и наглядные пособия: карточки с изображением 6 кругов.

Педагог раздает карточки с изображением 6 кругов, предложить закрасить их таким образом, чтобы закрашенных и не закрашенных фигур было поровну. Затем просмотреть и просчитать все варианты закрашивания.
Так же можно провести соревнование: кто найдет наибольшее количество решений.

Дидактическая игра «Что бывает…»
Цель: развивать логическое мышление.

Взрослый предлагает ребенку поочередно задавать друг другу вопросы следующего порядка:
— Что бывает большим? (Дом, машина, радость, страх и т. п.)
— Что бывает узким? (Тропа, лепта, лицо, улица и т. п.)
— Что бывает низким? Что бывает высоким?
— Что бывает красным? Что бывает белым? Что бывает желтым?
— Что бывает длинным? Что бывает коротким?

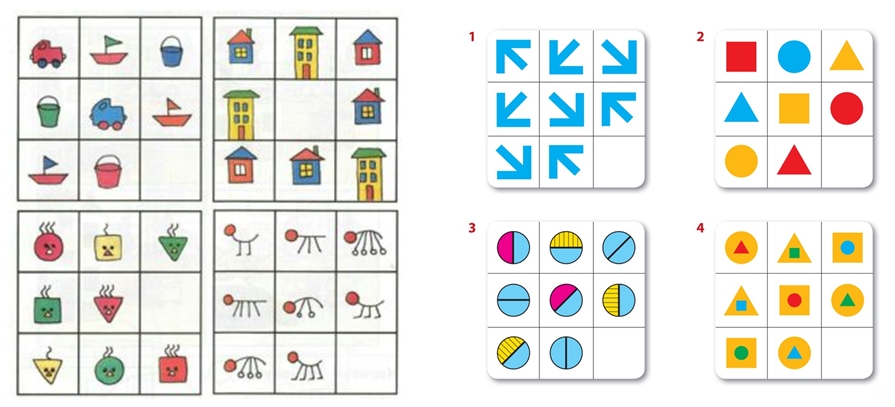
Дидактическая игра «Выбери подходящую картинку»

Дидактическая игра «Расположи предметы разными способами»

Дидактическая игра «Магические квадраты»
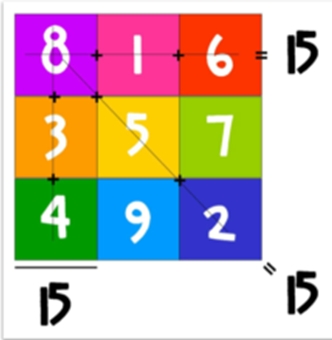Квадрат заполняется числами таким образом, что сумма чисел в каждом ряду по вертикали, горизонтали и диагонали  одинакова.

Для дошкольников чаще всего используют квадрат с изображением предметов.

Дидактическая игра «Подбери смысловую пару»

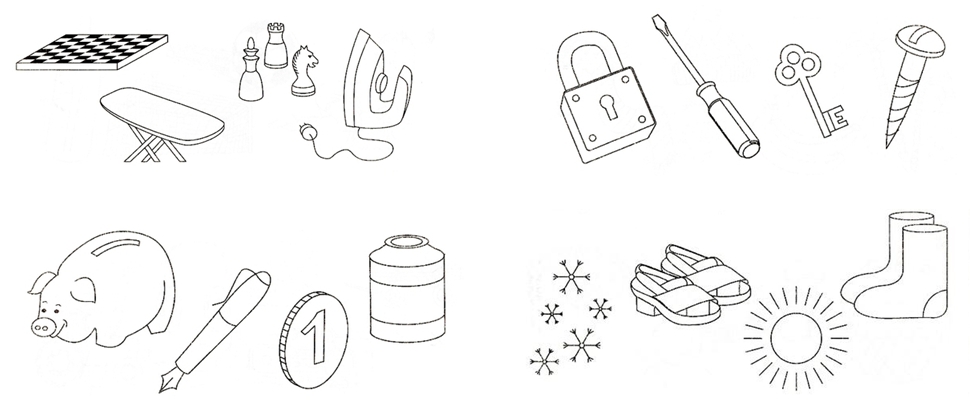
Дидактическая игра «Заполни таблицу»
Рассмотри рисунок. Догадайтесь, что обозначают знаки + и – в таблице.

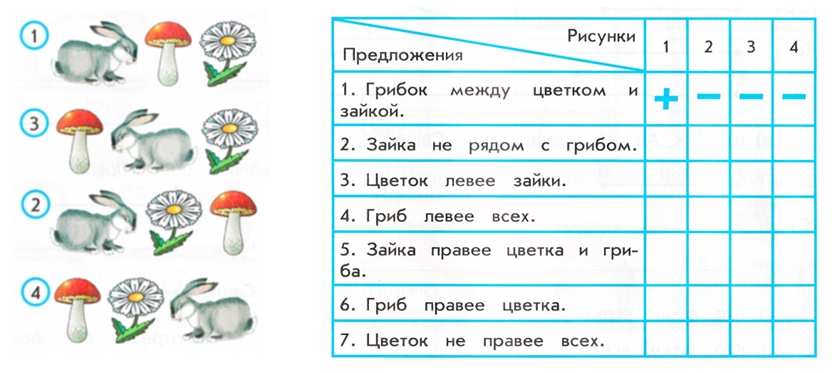
Дидактическая игра «Верно-ложно»
Рассмотри рисунок. Прочитай предложения в таблице и ответь верные и ложные.

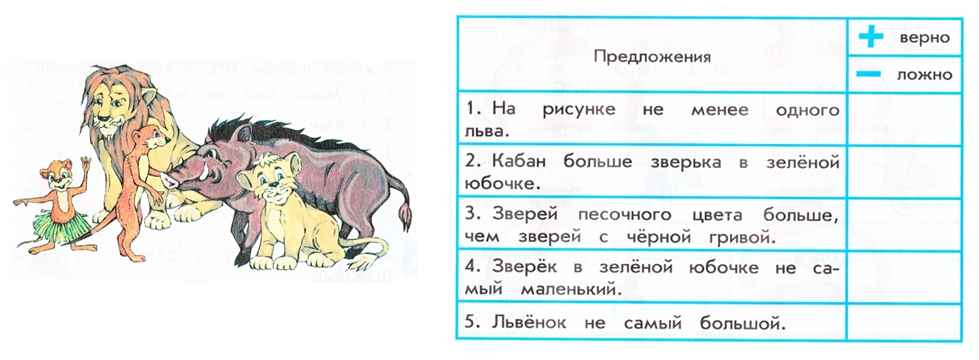
Дидактическая игра «Раскрась верно»
Раскрась зелёным цветом картинку, на которой нет мячика; синим цветом – ту, где нет пирамидки; красным – где нет кубика; жёлтым – где есть все предметы.

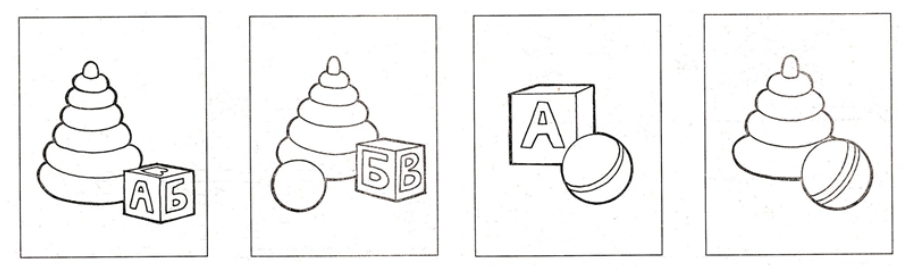
Дидактическая игра «Фотография»
На каком из четырёх рисунков герои изображены правильно?

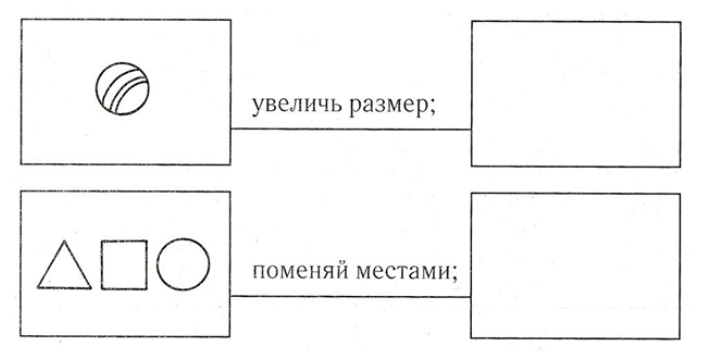
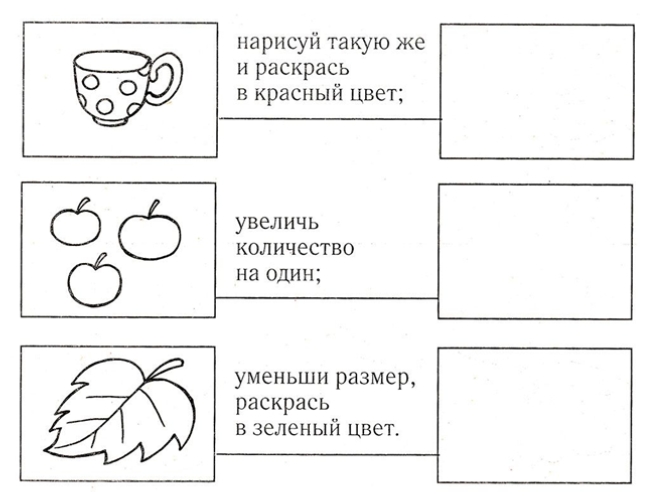
Дидактическая игра «Робот»
Выполни определённые действия

Логические задачки-картинки

Задача-картинка «Найди ошибки художника»
Исправь ошибки на рисунках.

Задача-картинка «Спрятанные картинки»

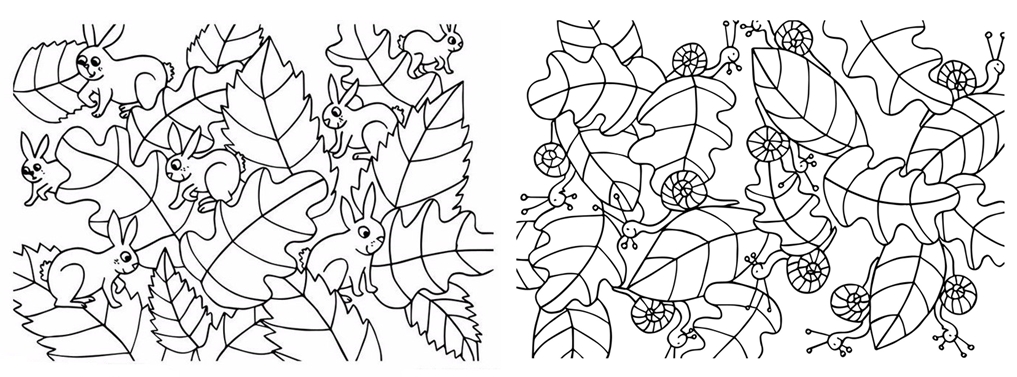
Задача-картинка «Где заяц?»
Ребята вышли в лес, чтобы покататься на коньках и на лыжах. Навстречу им выскочил заяц, испуганно присел и помчался дальше. Ребята погнались было за ним, но потеряли его из виду. А заяц-то никуда не убегал, он всё ещё на картинке. Найдёте?

Да вот же он! Между мальчиком и девочкой:

Задача-картинка «Встреча на улице»
Встретились на улице 2 друга:
– Здравствуй, Стёпа. Ты куда?
– Я иду в дом №23, – говорит Стёпа. – А ты куда, Петя?
– А я – к приятелю Ванюше. Он живёт в доме №7, – отвечает Петя.

Вот теперь скажите: кого из них зовут Стёпой, а кого Петей.
Стёпа – это мальчик в кепке. Почему?
Обратите внимание на номер дома – 19. Если идти от первого дома на улице, то дома с нечётными номерами будут на левой стороне, мальчик в кепке движется по направлению к домам с большими номерами, 23 больше, чем 19, а значит, это Стёпа.

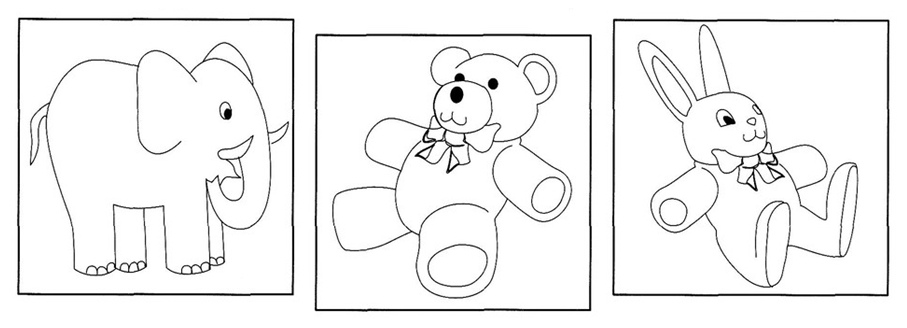
Задача-картинка «Самый большой»
Слон меньше мишки, а мишка меньше зайчика. Какая игрушка больше всех?

Задача-картинка «Чей Мурзик?»
На рисунке три подружки: Ира, Таня и Галя.
С ними кот Мурзик. Только вот чей он? Кто хозяйка Мурзика?

Ответ. Мурзик принадлежит Гале – девочке с одним бантом. Второй бантик она отдала Мурзику.

Задача-картинка «Имена кукол»
У кукол Ляли и Милы одинакового цвета платья, у Инны и Лизы – бантики, а у Милы и Лизы – туфельки.
Как зовут каждую куклу?
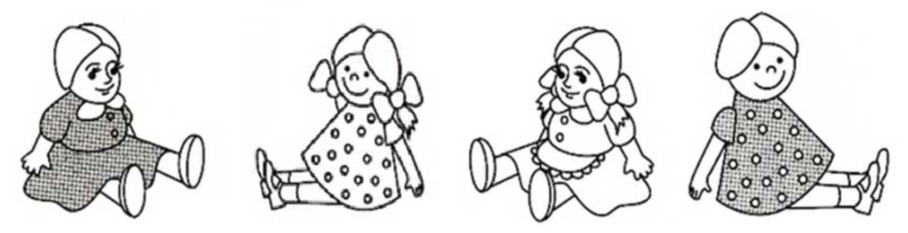Ответ. По порядку: Ляля, Лиза, Инна, Мила.

Задача-картинка «Кто что собирал»
Галя, Костя, Даша и Сережа собирали овощи. Трое собирали картофель, а кто-то один из них морковь. Галя и Сережа собирали разное, Сережа и Даша – тоже.

Ответ. Сережа – морковь, остальные картофель.

Задача-картинка «Что в коробке»
В красной коробке лежит не кукла и не юла. В зеленой – не юла и не дудочка. В желтой – не кукла и не дудочка. Какой предмет лежит в каждой из коробок?
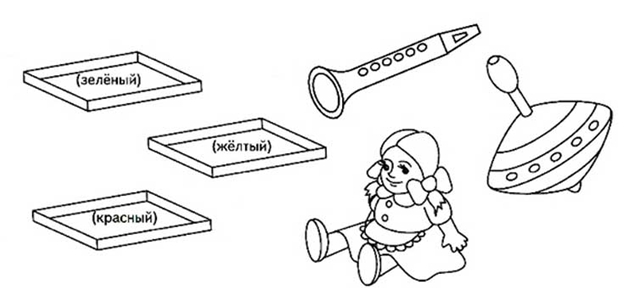Ответ. В красной – дудочка, в зеленой – кукла, в желтой – юла.

Задача-картинка «Кто где живет»
Жираф, крокодил и бегемот жили в разных домиках. Жираф жил не в зеленом и не в синем домике. Крокодил жил не в зеленом и не в желтом. В каких домиках жили звери?
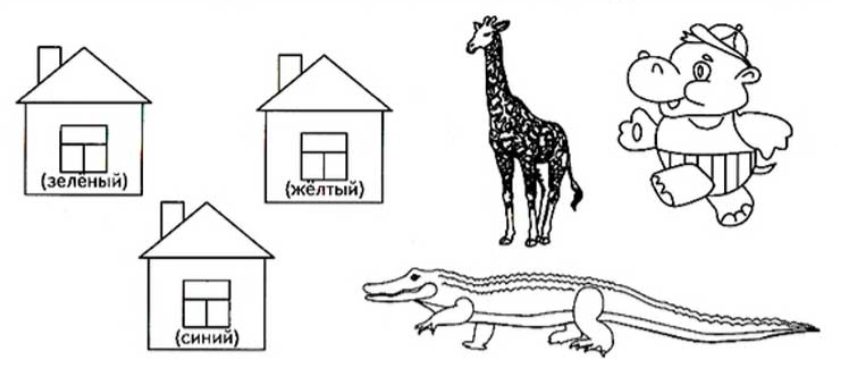Ответ. Жираф – желтый домик, крокодил – синий домик, бегемот – в зеленом.

Задача-картинка «Имена детей»
На рисунке пятеро ребят. Одного из них зовут Колей, и он стоит с краю. Если бы Нюра стояла рядом с Володей, то Петя оказался бы рядом со своим тёзкой. Кто где стоит?
Ответ. По порядку: Коля, Володя, Петя, Нюра, Петя.

Задачка-картинка «Поход»

1. Сколько человек проживает в лагере?
   В лагере проживает 4 человека.
   Это легко понять по количеству столовых приборов, или по графику дежурств на дереве.

2. На чем ребята сюда доехали?
   Ребята приехали сюда на лодке.
   Обратите внимание на вёсла, прислоненные к дереву.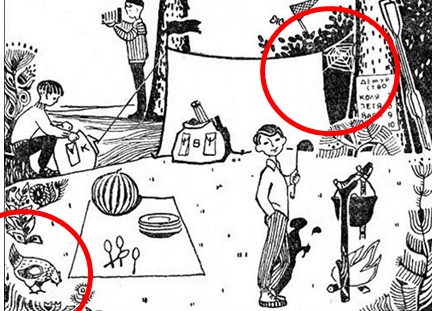
3. Сегодня ли они сюда приехали?
   Дети приехали сюда довольно-таки давно.
   Обратите внимание на паутину между деревом и палаткой. Паук не свил бы паутину так быстро.
4. Далеко ли расположен ближайший населенный пункт?
   Ближайшее поселение находится не очень далеко.
   Обратите внимание на домашнюю курицу в нижнем левом углу. Видимо, она пришла сюда из деревни.
5. Куда ушел мальчик, по имени Шура? Его на картинке не видно.
   Вот нам и дали подсказку по именам. Теперь мы знаем, что четвертого мальчика зовут Шура. Куда же он делся?
   Обратите внимание на сачок за палаткой. Следовательно, Шура ловит бабочек.
6. С какой стороны дует ветер? С юга или с севера?
   Во-первых, флажок на палатке показывает направление ветра. Слева-направо.
   Давайте разберемся, где находится север, а где юг. Обратите внимание на ели. Мы знаем, что еловые ветви с южной стороны всегда длиннее, чем с северной.
   Следовательно, юг расположен в левой части картинки, а север в правой.
   Следовательно, ветер дует с юга на север.
7. Какое в данный момент время суток? Вечер, полдень или утро?
   Определив направление сторон света, мы можем легко определить время суток по тени. Мальчик с поварешкой стоит лицом на север, значит по правую его руку у него восток, а по левую – запад. Его тень падает в западную сторону, следовательно, солнце находится на востоке, а значит сейчас утро.
8. Кто из мальчиков дежурил вчера? Назовите его имя.
   Как мы видим, рюкзаки мальчиков подписаны первыми буквами их имён.
   Мальчик по имени Коля (на его рюкзаке буква К), сидит с левой части картинки, и что-то ищет в рюкзаке.
   Рюкзак с буквой «В», принадлежащий Васе, лежит возле палатки. Из него торчит фотоштатив. Сам Вася стоит с фотоаппаратом и делает снимки.
   Шура, как мы знаем, ловит бабочек сачком.
   Следовательно, согласно графику дежурств сейчас дежурит Петя. А значит, вчера дежурил Коля.
9. Число и месяц, которые запечатлены на картинке.
   Число месяца вычислить легко. Нужно опять обратиться к графику дежурств. Сегодня восьмое число.
   Какой же месяц?
   Так как картинка советских времен, и импорт ягод и фруктов не был тогда развит настолько сильно, как сейчас, арбузы можно было купить лишь в августе. Так, как на картинке присутствует арбуз, следовательно, сейчас август. Итак, действия на картинке происходят восьмого августа.

Логические задачи

Грамматические примеры. Выполни действия и напиши полученное слово.

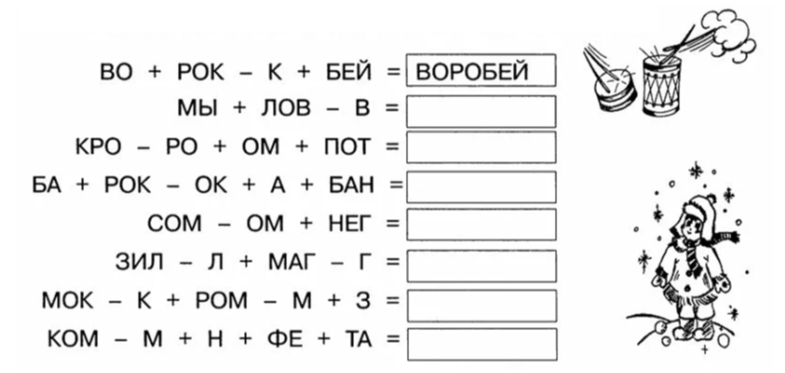
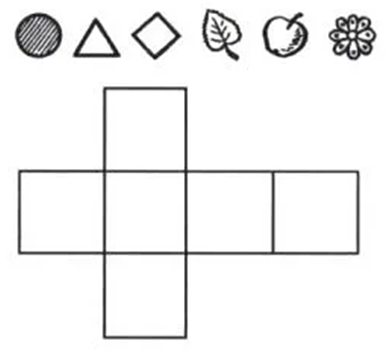На развертке куба расставь фигуры так, чтобы на противоположные грани попали:

• круг и треугольник;
• квадрат и ромашка;
• яблоко и лист.

Найди номер того кубика, который сделан из данной развертки.

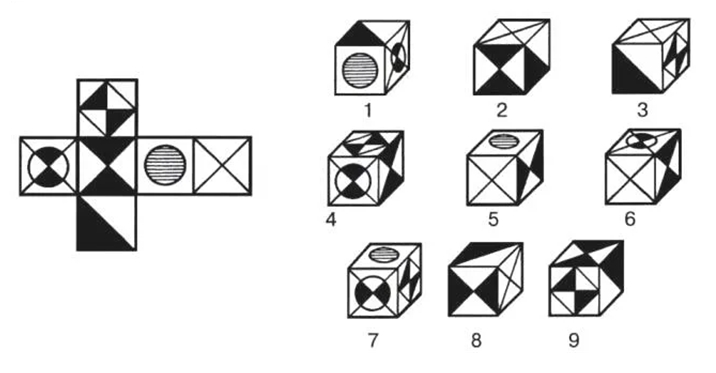
Узнай пословицу по рисунку.

Изографы

Изографы – это картинки, на которых слова нарисованы буквами, различным образом расположенные в пространстве и  оптически похожие на  предмет, в названии которого используются эти буквы. Ребенок должен найти все нарисованные буквы изографа, составить из них слово.

Методика работы с изографами.

1. Рассматривание изографа и нахождение всех букв, «спрятанных» в нём.
2. Визуальное определение предмета, зашифрованного в изографе.
3. Составление слова.
4. Определение орфограммы в этом слове.
5. Выкладывание слова из букв разрезной азбуки.
6. Записывание слова-изографа в тетради.
7. Называние букв и звуков слова-изографа.
8. Определение гласных и согласных букв в слове-изографе.
9. Разделение слова-изографа на слоги.
10. Зарисовка слова-изографа в тетради.
11. Отстукивание ритма слова-изографа.
12. Придумывание предложения со словом изографом.
13. Выкладывание из крупы одного из слогов слова-изографа.

Работа с изографом (примерные вопросы):
— Рассмотрите изограф. Какой предмет он напоминает?
— Составьте слово.
— Какая орфограмма спряталась в этом слове? Запишите это слово, выделив орфограмму.
— Произнесите слово и звуки, из которого оно состоит.

Прочитай слова и назови лишнее слово.

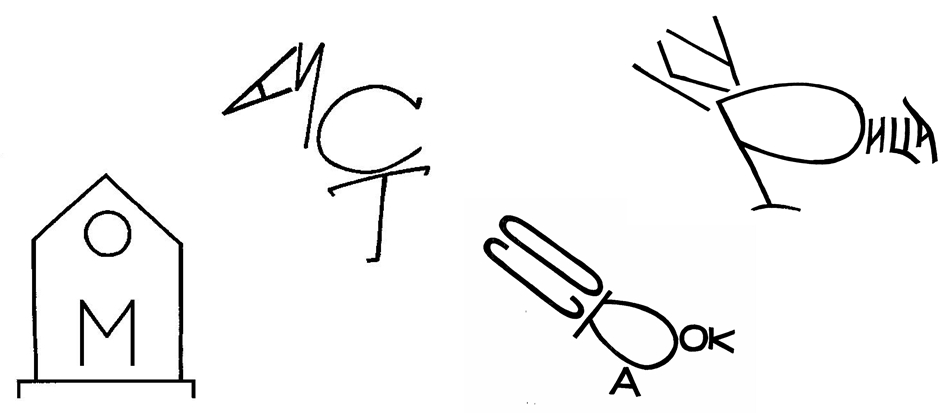
Логические игры со спичками

Головоломки со спичками – это великолепное развлечение, развивающее мелкую моторику рук, повышающее внимательность и усидчивость, формирующее логическое и образное мышление вашего ребёнка.

Играть со спичками можно даже в раннем возрасте. Начните с того, что просто складывайте вместе с ребёнком из спичек разные фигуры. Сначала – простые геометрические формы: квадрат, треугольник, ромб, звёзды. Затем переходите к более сложным образам (которые можно почерпнуть из наших головоломок или придумать самим): домик, рак, флюгер и т.п. Чтобы сделать это занятие ещё более увлекательным, возьмите вместо спичек разноцветные мелки или карандаши.

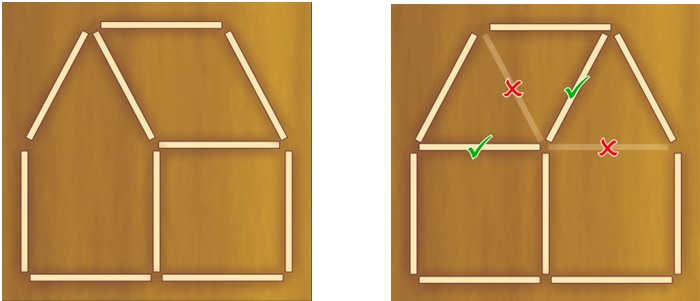
Дом из спичек
Из спичек построен дом.
Переложите две спички так, чтобы дом повернулся другой стороной.

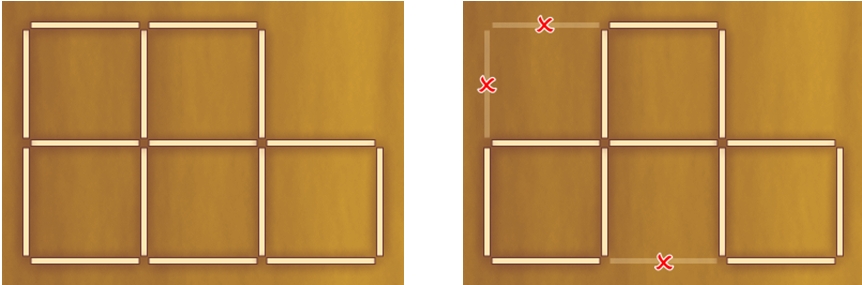
Из пяти квадратов – три
Из 15 спичек выложено 5 квадратов. 
Снимите 3 спички так, чтобы осталось три таких же квадрата.

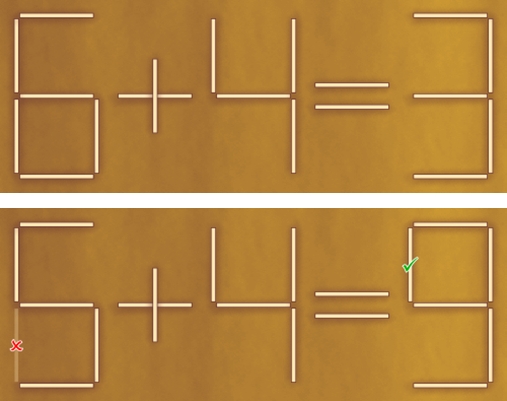
6 + 4 = 3
Переложите одну спичку так, чтобы равенство стало верным:

Из пяти треугольников – два
Из 9 спичек выложена фигура, в которой можно насчитать 4 маленьких и один большой треугольник.
Уберите 2 спички так, чтобы осталось только 2 треугольника.

Спичечные весы
Весы составлены из 9 спичек и не находятся в состоянии равновесия.
Переложите в них 5 спичек так, чтобы весы оказались в равновесии.

Использование логических блоков Дьенеша

В практике работы с детьми находит место два вида логического дидактического материала: объёмный и плоскостной – соответственно блоки и логические фигуры.

Что же представляет собой логические блоки Дьенеша?
Логический материал представляет собой набор из 48 логических блоков, которые различаются четырьмя свойствами:

• формой – круглые, квадратные, треугольные, прямоугольные
• цветом – красные, синие, желтые
• размером – большие и маленькие
• толщиной – толстые и тонкие.

К набору блоков прилагаются также карточки-символы:

• цвет – изображается пятном
• форма – контурами фигур
• толщина – условным обозначением человеческой фигуры: толстый – тонкий
• размер – силуэтами домиков: большой – маленький.

Всего 11 карточек. И 11 карточек с отрицанием свойств, например, не красный, не большой и т.д.

В наборе нет даже двух фигур, одинаковых по всем свойствам.

Конкретные варианты свойств (красный, синий, желтый, прямоугольный, круглый, треугольный, квадратный) и различия по величине и толщине фигур такие, которые дети легко распознают и называют.

Логические блоки Дьенеша:

• знакомят с формой, цветом, размером, толщиной объектов;
• развивают логическое мышление, представление о множестве, операции над множеством (сравнение, разбиение, классификация, абстрагирование);
• формируют представления о математических понятиях (алгоритм, кодирование и декодирование информации, кодирование со знаком отрицания);
• развивают умение выявлять свойства в объектах, называть их, адекватно обозначать их отсутствие, обобщать объекты по их свойствам (по одному, двум, трем), объяснять сходства и различия объектов, обосновывать свои рассуждения;
• развивают творческие способности, воображение, фантазию, способности к моделированию и конструированию, что в итоге развивает интеллектуально-творческие способности детей и позволяет сформировать у детей дошкольного возраста предпосылки к учебной деятельности.

Дидактическая игра «Магазин»
Материал: товар (карточки с изображением предметов); логические фигуры.
Цель игры: развитие умения выявлять и абстрагировать свойства; развитие умения рассуждать, аргументировать свой выбор.

Дети приходят в магазин, где представлен большой выбор игрушек. У каждого ребенка 3 логические фигуры «денежки». На одну «денежку» можно купить только одну игрушку.
Правила покупки: купить можно только такую игрушку, в которой есть хотя бы одно свойство логической фигуры. Правило можно усложнить выбор игрушки по двум свойствам (например, большой квадрат, синий квадрат и т. д.)

Дидактическая игра «Что изменилось»
Материал: набор блоков Дьенеша.
Цель игры: совершенствовать  знания детей о геометрических фигурах, их  цвете, величине, толщине; развивать мышление.

Перед ребенком на стол выкладывается несколько фигур, которые нужно запомнить, а потом одна из фигур исчезает или заменяется на новую, или две фигуры меняются местами. Ребенок должен заметить изменения.

Дидактическая игра «Хоровод»
Материал: набор логических блоков Дьенеша.
Цель игры: классифицирует блоки по двум – трем признакам: цвету, форме; цвету – форме – размеру.

Взрослый предлагает выстроить в веселый хоровод волшебные фигуры. Хоровод получится красивым и нарядным.
Блоки выкладываются по кругу. Произвольно берется любой блок, затем присоединяется блок, в котором будет присутствовать один признак предыдущего блока и так далее. Последний блок должен совпадать с первым блоком по одному какому – либо признаку. В этом случае игра заканчивается – «хоровод» закрыт.

Дидактическая игра «Второй ряд»
Материал: набор логических блоков Дьенеша.
Цель игры: развивать  умение анализировать, выделять свойства фигур, находить фигуру, отличную по одному признаку.

Выложить в ряд 5-6 любых фигур. Построить под ними второй ряд, но так, чтобы под каждой фигурой верхнего ряда оказалась фигура другой формы (цвета, размера); такой же формы, но другого цвета (размера); другая по цвету и размеру; не такая по форме, размеру, цвету.

Дидактическая игра «Найди клад»
Материал: набор блоков Дьенеша.
Цель игры: совершенствовать  знания детей о геометрических фигурах, их  цвете, величине, толщине; развивать мышление.

Выкладываем перед ребенком 8 логических блоков Дьенеша, и пока он не видит, под одним из них прячем «клад» (монетку, камешек, вырезанную картинку и т.п.). Ребенок должен задавать вам наводящие вопросы, а вы можете отвечать только «да» или «нет»: «Клад под синим блоком?» — «Нет», «Под красным?» — «Нет». Ребенок делает вывод, что клад под желтым блоком, и расспрашивает дальше про размер, форму и толщину. Затем «клад» прячет ребенок, а взрослый задает наводящие вопросы.
Затем в эту игру могут играть сами дети, соревнуясь в нахождении клада.

Дидактическая игра  «Игра с одним обручем»
Материал: обруч, комплект логических блоков Дьенеша.
Цель игры: развивать умение разбивать множество по одному свойству на два подмножества, производить логическую операцию «не».

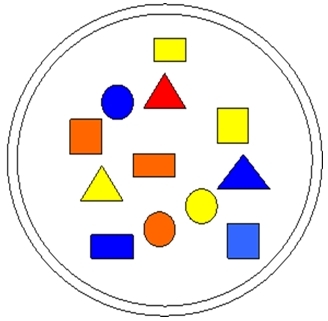Перед началом игры выясняют, какая часть игрового листа находится внутри обруча и вне его, устанавливают правила: например, располагать фигуры так, чтобы все красные фигуры (и только они) оказались вне обруча.
После расположения всех фигур предлагается два вопроса: какие фигуры лежат внутри обруча? Какие фигуры оказались вне обруча? (Ответ: «Вне обруча лежат все не красные фигуры»).
При повторении игры дети могут сами выбирать, какие блоки положить внутри обруча, а какие вне.

Дидактическая игра «Игра с двумя обручами»
Материал: 2 обруча, комплект логических блоков Дьенеша.
Цель игры: развитие умения разбивать множество по двум совместимым свойствам, производить логические операции «не», «и», «или».

Перед началом игры необходимо выяснить, где находятся четыре области, определяемые на игровом листе двумя обручами, а именно: внутри обоих обручей; внутри красного, но вне зеленого обруча; внутри зеленого, но вне красного обруча и вне обоих обручей (эти области нужно обвести указкой).

• затем называется правило игры. Например, расположить фигуры так, чтобы внутри красного обруча оказались все красные фигуры, а внутри зеленого все круглые
• после решения практической задачи по расположению фигур дети отвечают на вопросы: какие фигуры лежат внутри обоих обручей; внутри зеленого, но вне красного обруча.

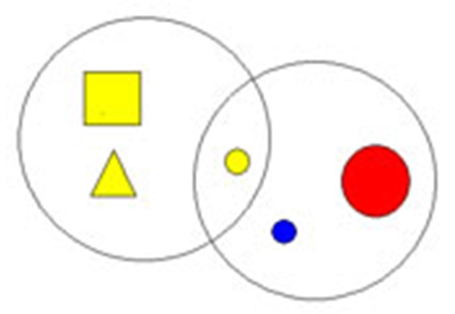Игру с двумя обручами целесообразно проводить много раз, варьируя правила игры.

Примечание: В вариантах 5 и 6 общая часть остается пустой. Надо выяснить, почему нет фигур одновременно красных и зеленых, а также нет фигур одновременно круглых и квадратных.

Дидактическая игра «Заселим в домики»
Материал: комплект логических блоков Дьенеша, таблицы с изображением дорожек и домиков
Цель игры: развивать  умение анализировать, выделять свойства фигур, классифицировать.

Перед детьми таблица № 1. Ребенку нужно помочь каждой фигуре попасть в свой домик, ориентируясь на знаки-указатели.

Дидактическая игра «На свою веточку»
Материал: комплект из 24 фигур (четыре формы, три цвета, две величины). Каждая фигура – носитель трех важных свойств: формы, цвета, величины, и в соответствии с этим название фигуры состоит из названия трех свойств: красный, большой прямоугольник; желтый, маленький круг; зеленый, большой квадрат и т. п.
Цель игры: развивать умение анализировать, выделять свойства фигур, классифицировать фигуры по нескольким признакам.

На рисунке изображено дерево, на котором должны «вырасти» фигуры. Чтобы узнать, на какой ветви какая «вырастет» фигура, возьмем, например, зеленый, маленький прямоугольник и начнем двигать его от корня дерева вверх по веткам.

Следуя указателю цвета, мы должны двигать фигуру по правой ветви. Дошли до разветвления. По какой ветви двигаться дальше? По правой, у которой изображен прямоугольник. Дошли  до следующего разветвления. Дальше елочки показывают, что по левой веточке должна продвигаться большая фигура, а по правой – маленькая. Значит, мы пойдем по правой веточке. Здесь и должен «вырасти» маленький зеленый прямоугольник. Так же поступаем с остальными фигурами. Аналогично проводиться игра со следующим рисунком.

Дидактическая игра «Цепочка»
Материал: набор логических блоков Дьенеша.
Цель игры: развитие умения анализировать, выделять свойства фигур, находить фигуру по заданному признаку.

От произвольно выбранной фигуры постарайтесь построить как можно более длинную цепочку.

Варианты построения цепочки:

1. Чтобы рядом не было фигур одинаковой формы (цвета, размера, толщины);
2. Чтобы рядом не было одинаковых по форме и цвету фигур (по цвету и размеру, по размеру и толщине и т.п.);
3. Чтобы рядом были фигуры одинаковые по размеру, но разные по форме и т.д.;
4. Чтобы рядом были фигуры одинакового цвета и размера, но разной формы (одинакового размера, но разного цвета).

Дидактическая игра «Помоги сказочному герою»
Цель игры: упражнять детей в группировке геометрических фигур; развивать наблюдательность, внимание и память.

Разделите  фигуры между сказочными  героями так:

• чтобы у  Буратино оказались все синие квадраты;
• чтобы Карандашу  достались все  желтые;
• чтобы Незнайке достались все желтые и большие.

Дидактическая игра «Этажи»
Материал: набор блоков.
Цель игры: развивать умение классифицировать и обобщать геометрические фигуры по признакам; упражнять в счете; развивать ориентировку в пространстве, внимание, логическое мышление.

Вариант 1: предлагаем выложить в ряд несколько фигур – 4-5 шт. Это жители первого этажа. Теперь строим второй этаж дома так, чтобы под каждой фигурой предыдущего ряда оказалась деталь другого цвета (или размера, формы).
Вариант 2: деталь такой же формы, но другого размера (или цвета).
Вариант 3: строим дом с другими деталями по цвету и размеру.

Дидактическая игра «Найди меня»
Материал: набор блоков, 3 экземпляра кодовых карточек (2 – с обычным кодом, 1 – с кодом отрицания).
Цель игры: развитие умение читать кодовое обозначение геометрических фигур и находить соответствующий код.

Дети делятся на две группы. Одна берет карточки, другая – блоки. Дети первой группы по очереди читают (раскодируют) карточки, ребенок из второй группы, у которого оказался соответствующий блок, выходит и показывает геометрическую фигуру.

Возможно использовать слова:
«Блоки, блоки разные 
Желтые, синие и красные,
Всем нам они знакомые,
Найдите меня!»

Дидактическая игра «Улитка»
Материал: игровое поле с изображением спирали или цветная тесьма, набор блоков.
Цель игры: упражнять детей в классификации блоков по двум признакам; цвету и форме.

Педагог предлагает построить детям домик для улитки из волшебных фигур. Домик получится нарядным и красивым. Выкладывание блоков начинается с середины спирали. Произвольно берется один блок, затем присоединяется блок, в котором будет присутствовать один признак предыдущего блока.

Дидактическая игра «Домино»
Материал: блоки Дьенеша.
Цель игры: развивать умение выделять свойства геометрических фигур.

В эту игру можно играть нескольким участникам одновременно (но не более 4х). Блоки делим поровну между игроками. Каждый делает ход по очереди. Если фигуры нет, нужно пропустить ход. Побеждает тот, кто первым выложит все фигуры.
Как ходить?
Фигурами другого размера (цвета, формы).
Фигурами того же цвета, но другого размера или такого же размера, но другой формы.
Фигурами другого размера и формы (цвета и размера).
Такими же фигурами по цвету и форме, но другого размера.
Ходим фигурами другого цвета, формы, размера, толщины.